Relaciones en movimientos curvilineos

En los movimientos curvilineos pordemos relacionas las siguientes expresiones:

• Rapidez Lineal/Rapidez Angular
• Aceleración Centrípeta/Rapidez Lineal
• Aceleración Centrípeta/Rapidez Angular.
• Fuerza Centrípeta/ Rapidez Lineal
• Fuerza Centrípeta/ Rapidez Angular
• Ecuación de Transmisión del Movimiento

Rapidez Lineal/Rapidez Angular

Estas son directamente proporcionales, la rapidez lineal con la angular; ya que:

              
                 ∆α/∆T . r  = ∆s/∆T



Aceleración Centrípeta/Rapidez Lineal

El vector de aceleración centripeta y el cambio de vector de velocidad tangencial se relaciona de la siguiente forma:

                      

                                  a_c = ∆v / ∆t

La ecuacion implica que el vector aceleracion centripeta tiene la misma direccion y el mismo sentido que el cambio de velocidad.

                 

Fuerza Centrípeta/Rapidez Angular.

Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeda, representada por un vector dirigido hacia el centro de la circunferencia dado por:

  

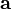 es la aceleración centrípeta.

 es el módulo de la velocidad.

 es el radio de la trayectoria circular (en general, el radio de curvatura).

 el vector de posición.

 el versor radial.

        la velocidad angular. 

Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración. Así, si consideramos una partícula de masa  en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:

Fuerza Centrípeta/ Rapidez Lineal

• 
  La aceleración centrípeta por ser un vector, está definida cuando se conoce su dirección y sentido. Se observa que por ser la dirección y sentido de la aceleración centrípeta, los mismos que los del vector ▲V se concluye que la dirección es radial y de sentido hacia el centro de la trayectoria en cada punto de ella.
  Se puede notar que la velocidad 
  y la aceleración
  
  en cada punto de la trayectoria son perpendiculares.
  
  
  
  
  

• 
  
  
  Aceleración Centrípeta/ Rapidez Angular
  Ya antes habíamos establecido  que el
  producto de la rapidez angular con el desplazamiento angular expresado en radianes es igual a la rapidez lineal.
  Por lo tanto podemos establecer la siguiente ecuación:
  
  
  
  
  • Ecuación de Transmisión del Movimiento
    
    La polea sirve para transmitir una fuerza, esta se 
    trata de una rueda, generalmente maciza y acanalada  
    en su borde, que, con el concurso de una rueda, se usa como elemento de transmisión para cambiar la dirección del movimiento en máquinas y mecanismos. "el número de revoluciones de las dos ruedas es inversamente proporcional al radio de ellas".
                                           
    
    Los engranajes emplean un movimiento giratorio o alternativo desde una parte de una maquina a otra.
    Un conjunto de dos o más engranajes que transmite el movimiento de un eje a otro se denomina tren de engranajesExisten tipos de engranajes como el simple y helicoidales